Discovering faster matrix multiplication algorithms with reinforcement learning

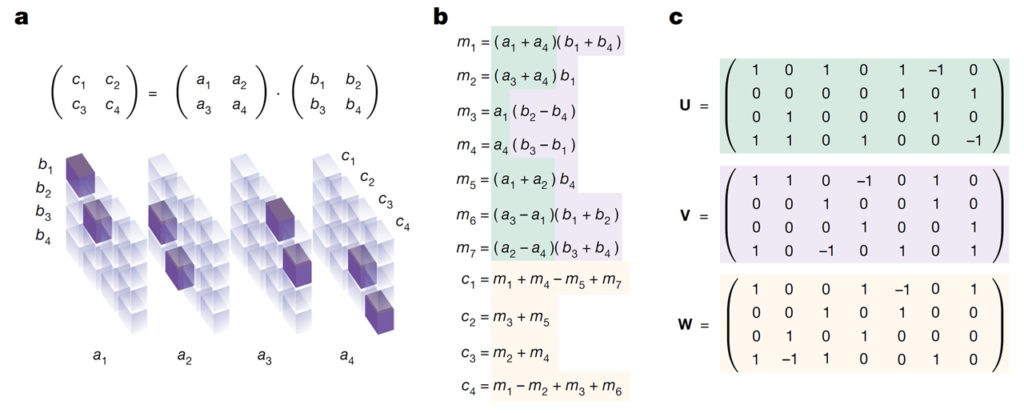
기본적인 계산을 위한 알고리즘의 효율성을 높이는 것은 전체 계산 속도에 영향을 주기에 광범위한 영향을 미칠 수 있습니다. 행렬 곱셈은 신경망에서 과학적인 컴퓨팅 루틴에 이르기까지 많은 시스템에서 사용하는 기초적인 작업 중 하나입니다. 머신러닝을 사용한 알고리즘의 자동화된 검색은 인간의 직관을 넘어서 지금까지 설계된 알고리즘 중 최고의 알고리즘을 능가할 가능성이 있습니다. 그러나 알고리즘 발견 절차를 자동화하는 것은 가능한 알고리즘의 공간이 방대하기 때문에 복잡합니다. 우리는 임의 행렬의 곱셈을 위한 효율적이고 입증 가능하며 올바른 알고리즘을 찾기 위해 AlphaZero를 기반으로 하는 심층 강화 학습 접근 방식을 이용했습니다. 우리 에이전트인 AlphaTensor는 finite factor space 내에서 텐서 분해를 찾는 싱글 플레이어 게임을 하도록 훈련되었습니다. AlphaTensor는 다양한 행렬 크기에 대해 최첨단 복잡성을 능가하는 알고리즘을 발견했습니다. AlphaTensor의 알고리즘이 50년 전에 발견된 이래 처음으로 Strassen의 2단계 알고리즘을 개선한 유한 필드의 4 × 4 행렬과 관련이 있습니다. 우리는 다양한 이용 사례를 통해 AlphaTensor의 유연성을 추가로 보여주었습니다. 구조화된 행렬 곱셈을 위한 최첨단 복잡성을 가진 알고리즘과 특정 하드웨어에서 런타임에 대한 행렬 곱셈을 최적화하여 실용적인 효율성을 개선했습니다. 우리의 결과는 다양한 문제에 대한 알고리즘 발견 프로세스를 가속화하고 다양한 기준에 맞게 최적화하는 AlphaTensor의 능력을 강조합니다.